Example-1 Strong and nonlocal sequence-dependence of the ground state shape are easily observed, especially in the 2D Plots pane. For example try comparing the 19 bp fragments

which all only differ in the composition of one base. Note also, that even for the uniform poly(A) sequence A_9 A [A] A_8 = A_19 (where the first input format allows centring of the 3D view on the 11th base pair) the local ground state configuration is (as it should be) different between the interior and regions close to the ends, with differences sometimes still visible three or four base pairs or more from an end.

Example-2 Another example of strong and nonlocal sequence-dependence of the ground state is to compare the change in the groundstate on asymmetric methylation or hydroxymethylation of CpG step (asymmetric when only one C in CpG step is modified). Note that this asymmetric modification of CpG step is arguably a smaller chemical change than a point mutation. For example, try comparing the four sequences

which all only differ in the composition of one base. Once again, a strong nonlocal sequence-dependence in the groundstate can be observed with methylation and hydroxymethylation of CpG step resulting in a similar change in the groundstate.

Example-3 Strong intrinsic bends can be observed for some sequences, e.g. with phased A-tracts such as

Then the effect of epigenetic modifications of CpG steps can be seen as even strong bend on the groundstate of the same sequence by simply replacing CG by MN

Example-4 Another interesting example is to compare the same sequence but for various dsNAs. For instance, poly(AT). Type GC(AT)_100GC in three different input forms but choose three different parameter sets, one for each kind of dsNAs supported by cgNA+web. Note that the choosing "RNA PS2" will internally convert T to U and "DRH PS2" only accepts input sequence in {A,T,C,G} as the DNA strand is chosen as the reading strand. Comparing the 3D structures for these three dsNAs, one can observe few standard characteristics of these dsNAs. For dsDNA (owing to the B-form geometry), the base-pairs are almost centred over the helical axis in contrast to dsRNA (which prefers A-form geometry), base-pairs are displaced away from the central helical axis and are closer to the major groove resulting in a ribbon-like helix with a more open cylindrical core. Whereas, DRH is somewhere in between dsDNA and dsRNA structure with a narrow open cylindrical core. Then all three 3D structures are intrinsically straight with different helical axis and are of different lengths. The total length of the 3D structures is in the order dsDNA > DRH > dsRNA related to their B-form, mixed A-B form, and A-form geometry. On average, the observed rise in A-form helices is significantly smaller than B-form helices. In the same example, it is also interesting to look at the 2D plots (try smaller sequences for easy visulation) in which one can observe striking differences in the cgNA+ internal coordinates due to A/B form geometry.

Example-5 And the sometimes significant consequences of reconstructing the same sequence with different parameter sets can be observed by comparing reconstructions of a single sequence with two different parameter sets, e.g. reconstructing the same dsDNA sequence with parameter sets DNA PS2 and cgDNA (old model) will provide a comparison between ground state reconstruction between the cgDNA (implicit phosphates) and cgNA+ (explicit phosphates) models. Moreover, for dsDNA, we have provided two cgNA+ parameter sets (DNA PS1 and DNA PS2) trained on the identical training sequences but simulated using two different MD protocols (details of the MD protocol are described below in Parameter sets section). See cgNA+ model pane to visualize how accurate is cgNA+ model when compared with the corresponding MD estimates, in particular, accurately capturing the small differences between the two different MD protocols.

The cgNA+ model

cgNA+ is a sequence-dependent, coarse-grain, model for double stranded nucleic acids (dsNA), which includes an explicit description of bases and phosphate groups, each approximated as a rigid body. For a complete description of the model see the cgDNA website, and the publications described there, particularly the PhD thesis of A. Patelli and R. Sharma. Briefly, given an arbitrary input sequence in the standard alphabet {A,T,C,G,U} and non-standard alphabets for epigenetically modified CpG steps {MN, MG, CN, HK, HG, CK}, (along the reading, or Watson, strand in the 5'-3' direction) with one of the provided parameter sets appropriate to chosen sequence, the cgNA+ model predicts a Gaussian (or multi-variate normal) probability density function (or PDF) for the dsNA configuration expressed in internal dsNA coordinates (more specifically a version of the standard Curves+ helicoidal coordinates for the relative rigid body displacements between bases, and an additional three translation and three rotation coordinates for the relative rigid body displacement between the base and phosphate group making up each nucleotide). The cgNA+ coarse-grain model is itself a slightly finer-grain evolution from the prior cgDNA coarse-grain model, which did not include an explicit treatment of the phosphate groups.

cgNA+ coordinates

In the cgNA+ model each interior (i.e. neither the first nor last) base pair level is approximated by four rigid bodies, specifically two (non-rigid) nucleotides each made up of a (rigid) base and a (rigid) phosphate group (but the two 5' phosphate groups are omitted from the first and last base pair levels). (The sugars are of course explicitly present in any MD simulation, but they are only implicit in the cgNA+ coarse graining.) Each additional interior dinucleotide step, or base pair junction, between adjacent base pair levels, adds 24 additional coarse grain coordinates; twelve familiar and standard coordinates namely (a Curves+ implementation of the Tsukuba convention for) six intra base pair coordinates (buckle, propeller, opening, shear, stretch, stagger) and six inter base pair (or junction) coordinates (tilt, roll, twist, shift, slide, rise), plus two, less familiar, analogous sets of relative rotations and translations (η₁, η₂, η₃, w₁, w₂, w₃) serving to locate each phosphate group, one in each backbone, with respect to the base within its nucleotide. The cgNA+ units of translations are Angstroms and for rotations fifth radians (or approximately 11.5 degrees). This nonstandard choice of unit for rotations is for reasons of good numerical scaling internal to the model, but for the sake of familiarity cgNA+web can also output rotational coordinates converted to degrees.

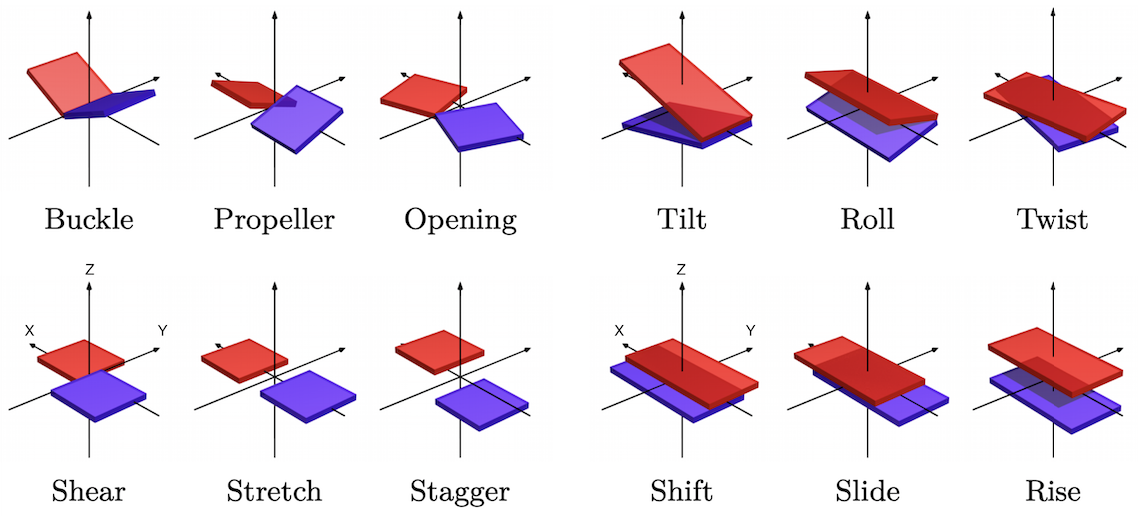
Schematic of CURVES+ coordinates of a coarse-grain DNA configuration with positive values of each coordinate shown. On right Inter base-pair variables: top, three Cayley rotation vector coordinates, bottom three translation vector components, all expressed in the halfway, junction frame. X axis toward reading strand back-bone, Y axis into major groove, Z axis approximately in the 5'-3' orientation of the reading strand, or equivalently toward base pair level a+1 from base pair level a. On left intra base pair coordinates, again three rotation and three translation components now expressed in the half way or base pair frame, and with the rigid body displacement being from the non-reading to the reading strand.

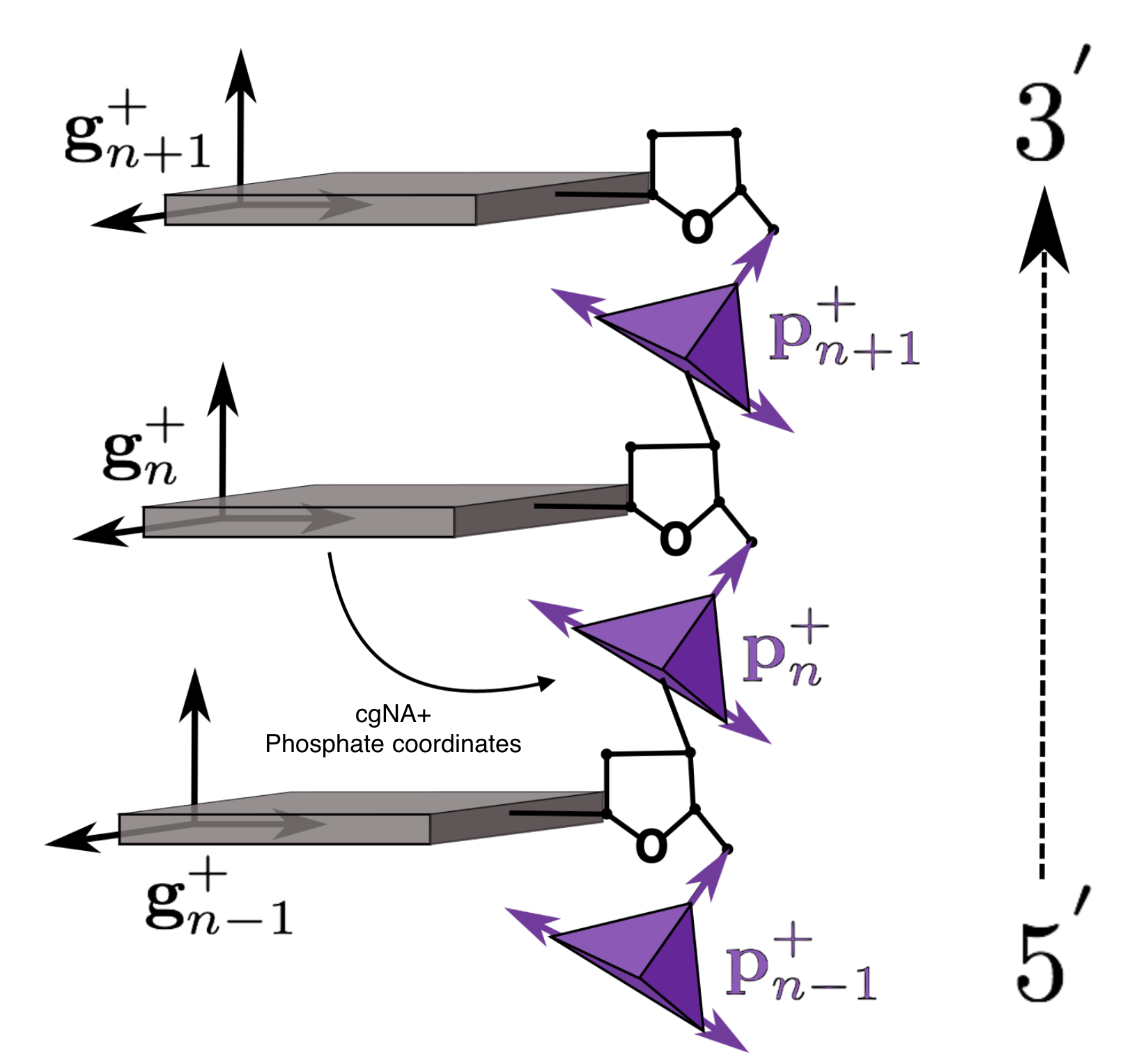
Schematic representation of the reading strand (denoted by subscript +) of a coarse-grained DNA fragment. cgNA+ phosphate coordinates are now an additional three rotation and three translation coordinates of the 5' phosphate group expressed in its associate base frame (as indicated by the arrow). Note that in the figure the sugar ring is shown but is only treated implicitly in the cgNA+ model.

Comparison of cgNA+ predictions with Molecular Dynamics simulations

cgNA+ parameter sets are trained on extensive atomistic MD simulations using state-of-the-art MD simulation protocol, and the model accurately captures the underlying sequence-dependent mechanics of dsNAs. The model have been tested throughly for numerous diverse sequences including A-tracts, CpG islands, random sequences, poly(A), and poly(AT).

Here, in Figure 1, we have shown results for one random sequence GCATTACGCTCCGGAGCGTAATGC that is outside the training library and contains all dimer steps at least once on the reading strand. Firstly, one can observe a strong sequence dependence in the groundstate coordinates, and more importantly, the cgNA+ model accurately captures this underlying sequence dependence in the groundstate of various kinds of dsNAs. Notably, the error between MD and model (dashed versus solid lines) is always significantly smaller than the variation along the sequence. Some of the interesting features of various dsNAs can also be observed; for instance, slide and twist for DRH are in between dsDNA and dsRNA. The phosphate coordinate η2 for dsRNA and dsDNA are strikingly different (can be attributed to the general A- and B-form of dsRNA and dsDNA, respectively) whereas η2 Watson phosphate rotational coordinate (i.e. DNA strand of DRH) is close to pure dsDNA while the same coordinate for Crick phosphates (i.e. RNA strand of DRH) is close to pure dsRNA.

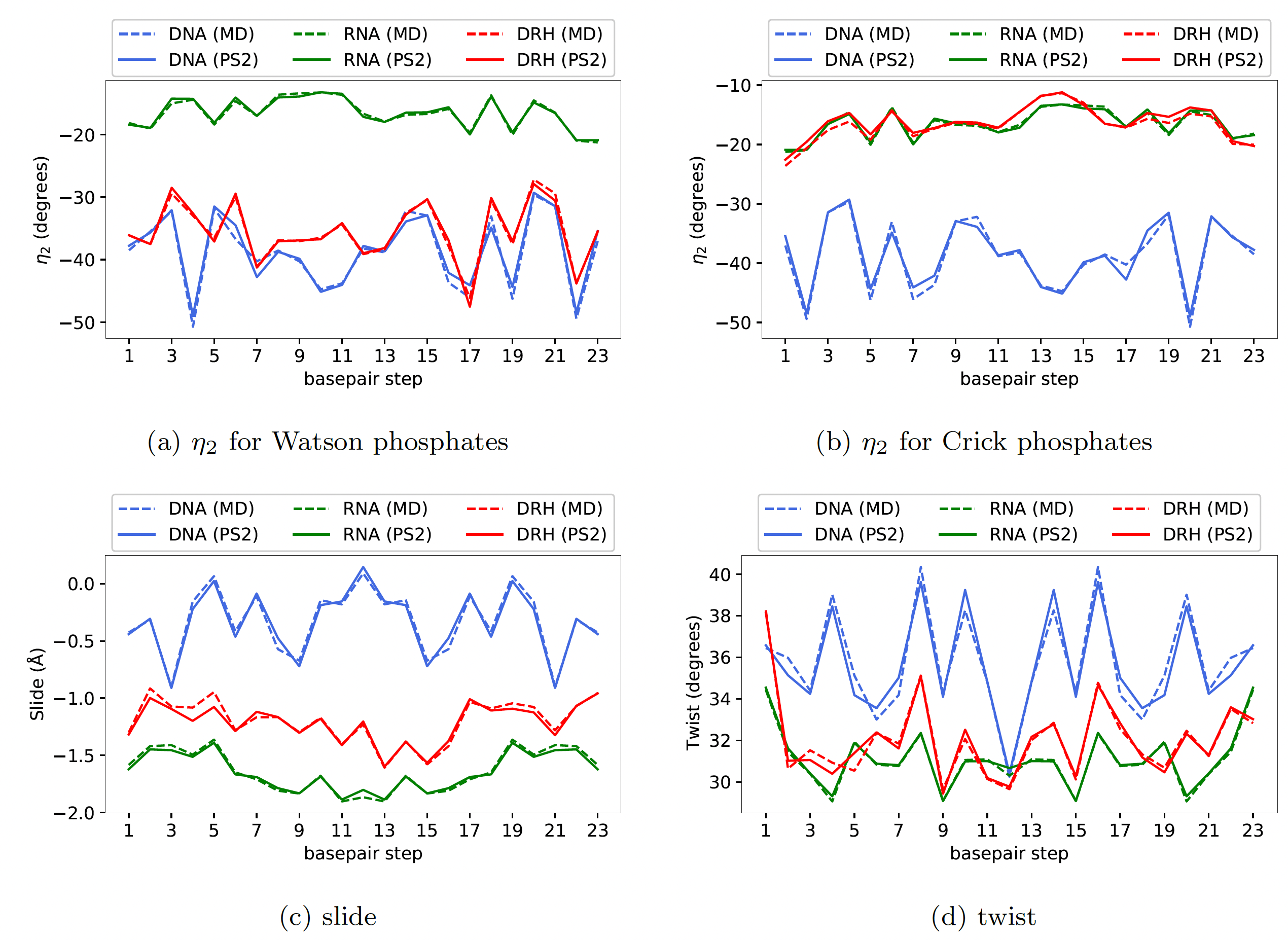
Figure 1 For the ground states of a 24mer sequence GCATTACGCTCCGGAGCGTAATGC (not in the training library and containing all dinucleotide steps), with versions for dsDNA (blue), dsRNA (green) and DRH (red), plots of (a) the η2 rotation coordinate for Watson-strand phosphates, (b) η2 for Crick-strand phosphates, (c) slide, and (d) twist, with solid lines being the cgNA+ model predictions, and dashed line data being taken directly from atomistic MD simulation. In all cases the error between MD observations and cgNA+ predictions is negligible compared to variation with sequence. (Data for other coordinates and other sequences entirely analogous.)

cgNA+ parameter sets, trained on extensive atomistic MD simulations using state-of-the-art MD simulation protocol, accurately captures the underlying sequence-dependent mechanics of dsNAs (see Figure 1); however, it should be noted that different MD protocols may lead to different atomistic equilibrium distributions, which also get reflected in cgNA+ parameter sets. In Figure 2, we have plotted the average shape of a dsDNA sequence observed in MD simulations but simulated using two different MD protocols (MD1 and MD2) along with the corresponding cgNA+ predictions (the parameter sets are available as ‘DNA PS1’ and ‘DNA PS2’ on the cgNA+web) trained on the same training sequences. The differences between the two MD protocols are in the water model, ion model, and length of the MD simulations for each training sequence which are SPC/E, Dang, and 3 μs for MD1 and TIP3P, Joung and Cheatham ion model, and 10 μs for MD2. More details on the MD protocol are provided in Get Started pane. For this particular sequence, the average shape observed in two MD simulations is considerably different, but the corresponding cgNA+ predictions are almost indistinguishable from the underlying MD estimates.

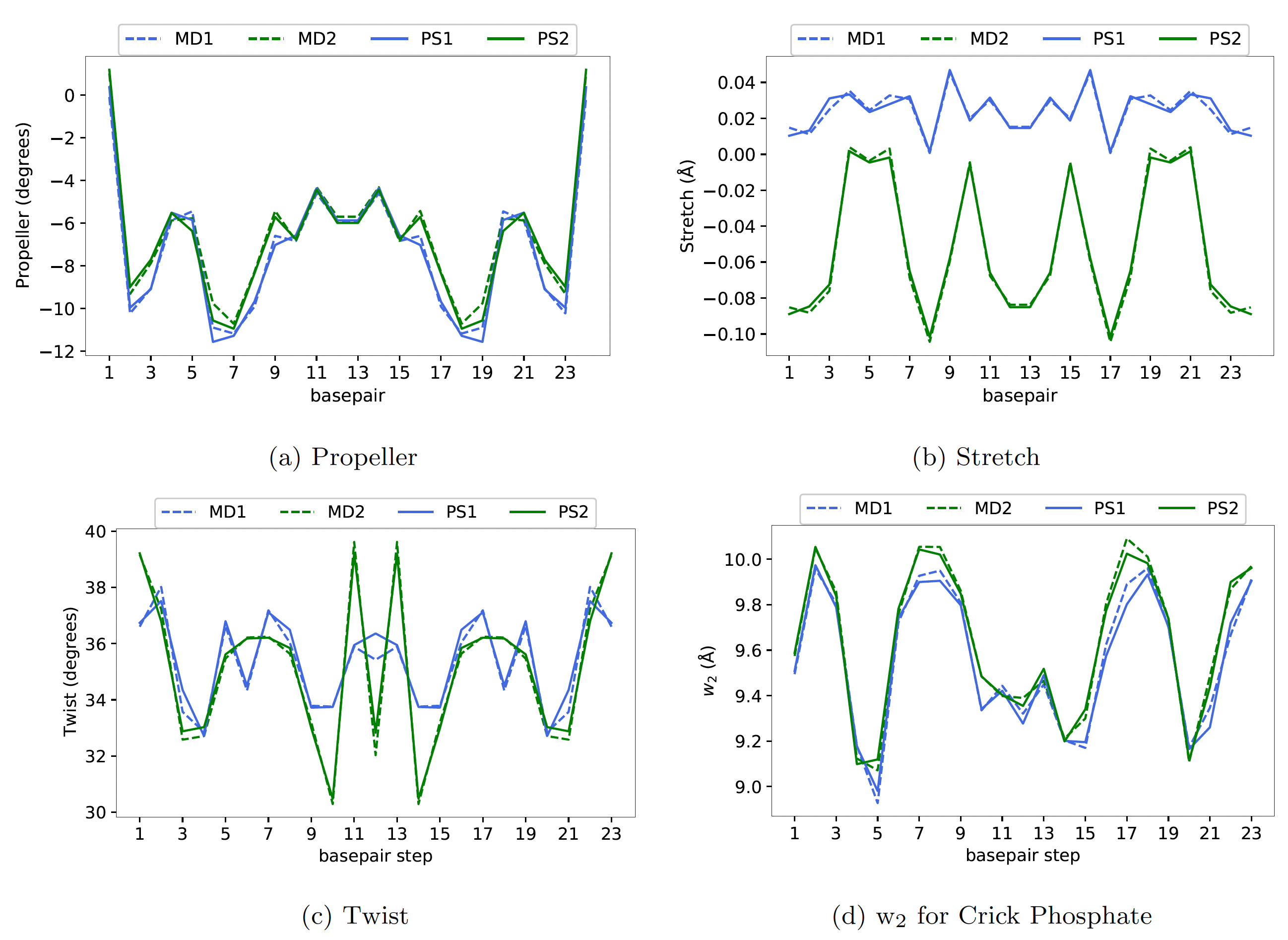
Figure 2 Plots of (a) Propeller, (b) Stretch, (c) Twist, and (d) w2 for Crick Phosphate for a dsDNA sequence (GCCTAACCCTGCGCAGGGTTAGGC) along the average shape observed in MD simulations using two different MD protocols (MD1 and MD2) and cgNA+ predictions for the two corresponding parameter sets PS1 and PS2. The differences for the two protocols is larger than the error between cgNA+ predictions and MD observation. Other coordinates similar.

More examples can be found in

cgNA+: A sequence-dependent coarse-grain model of double-stranded nucleic acids.
R. Sharma, EPFL Thesis #9792, Under the supervision of J. H. Maddocks
Download the PDF here.

cgNA+ vs cgDNA

The cgNA+ coarse-grain model is a finer-grain evolution from the prior cgDNA coarse-grain model. The cgDNA model did not include an explicit treatment of the phosphate groups i.e. it predicts the sequence-dependent Gaussian pdf in base coordinates only. Along with a finer description (both phosphate and base) of the dsNA, the cgNA+ model better captures the underlying MD statistics for base coordinates, as shown in figures below (taken from A. Patelli's thesis).

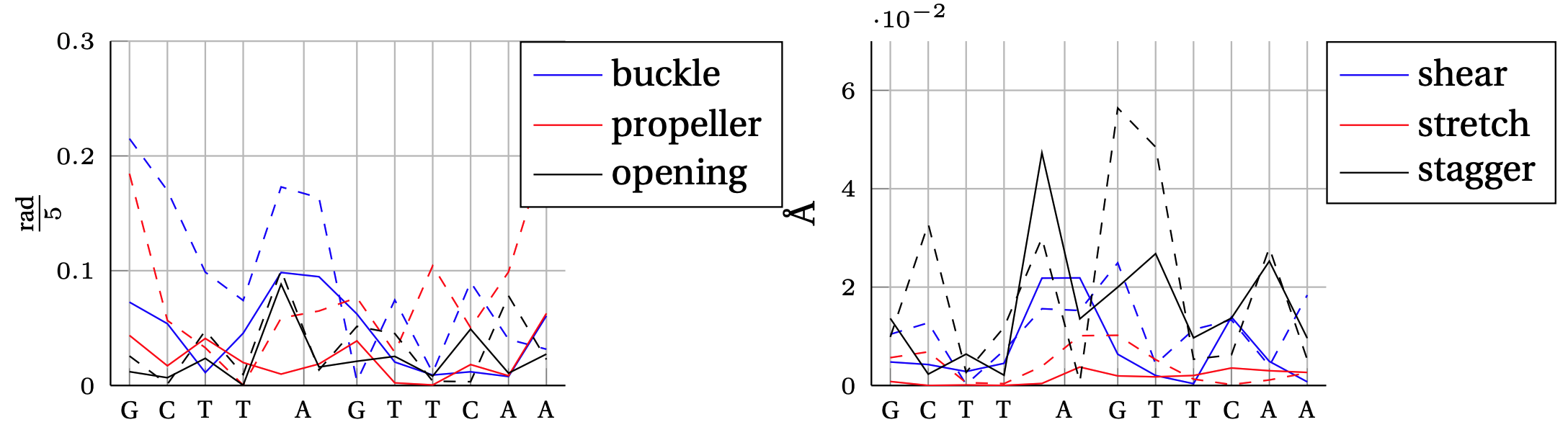
Absolute error between model predicted intra–base–pair degree of freedom and MD observation. In solid, we show the error obtained by the cgNA+ model (DNA PS1) and in dashed line the error obtained by the cgDNA (old) model.

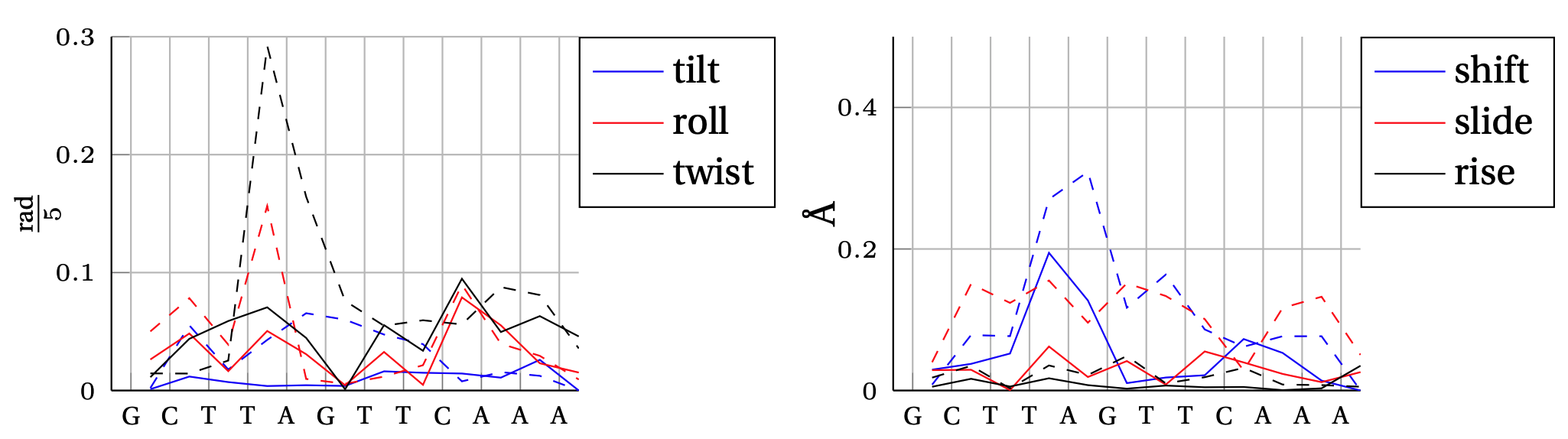
Absolute error between model predicted inter–base–pair degree of freedom and MD observation. In solid, we show the error obtained by the cgNA+ model (DNA PS1) and in dashed line the error obtained by the cgDNA (old) model.

Stiffness matrices

Figure 3 Sparsity pattern in observed stiffness matrix in MD simulation of a dsDNA sequence GCTTAGTTCAAATTTGAACTAAGC (only half sequence is shown as the sequence is a palindrome). The green stencils correspond to the nearest-neighbor interactions approximation. The dimension of the stiffness matrix is 558 X 558 (24n-18 where n=24 for this sequence) and x and y labels are the coordinate index.

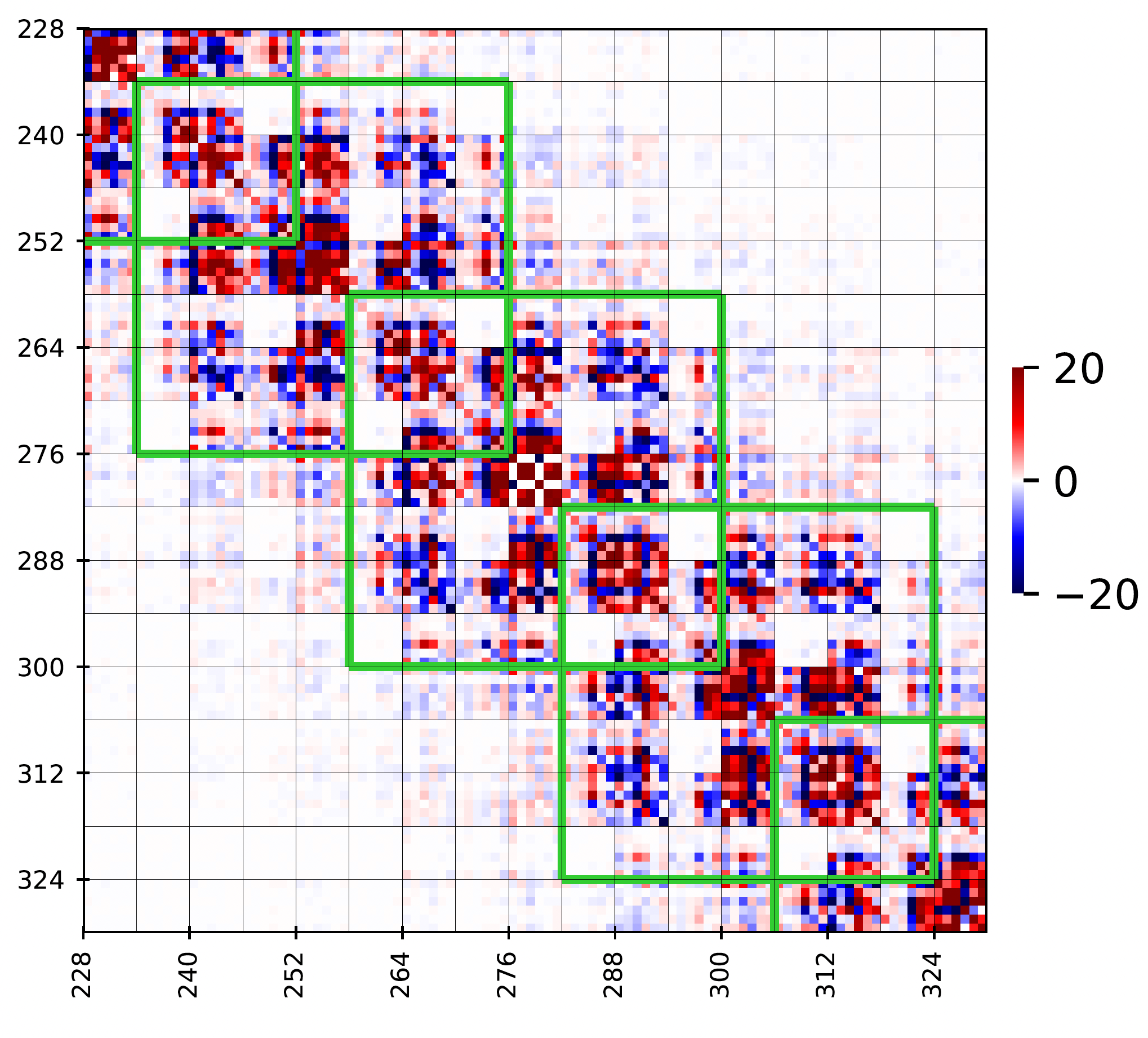
Figure 4 Zoom-in image of the above matrix corresponding to the central tetramer. The green stencils correspond to the nearest-neighbor interactions approximation.

The cgNA+ model predicts both a ground state configuration and a banded stiffness matrix for each input sequence. However cgNA+web focuses on visualising the ground state shape in various ways, and only provides the stiffness matrix via download of a file with its numerical entries. This data may then be post-processed as wished. One possibility is to make plots of the eigenvalues of the stiffness matrix, as indicated in the figure below (in the scaling with translation variables in Angstroms and rotations in 1/5th radians). Another is to download and use the .txt ground state shape and associated .csc/.json stiffness matrix as inputs to a Monte Carlo simulation code for sampling the cgNA+ Gaussian PDF in order to compute various expectations of interest, e.g. sequence-dependent persistence lengths as described in [6]. However, for extensive post-processing simulations it is probably more efficient to install and use the available cgNA+ Matlab/Octave or Python scripts directly rather than using the cgNA+web interface.

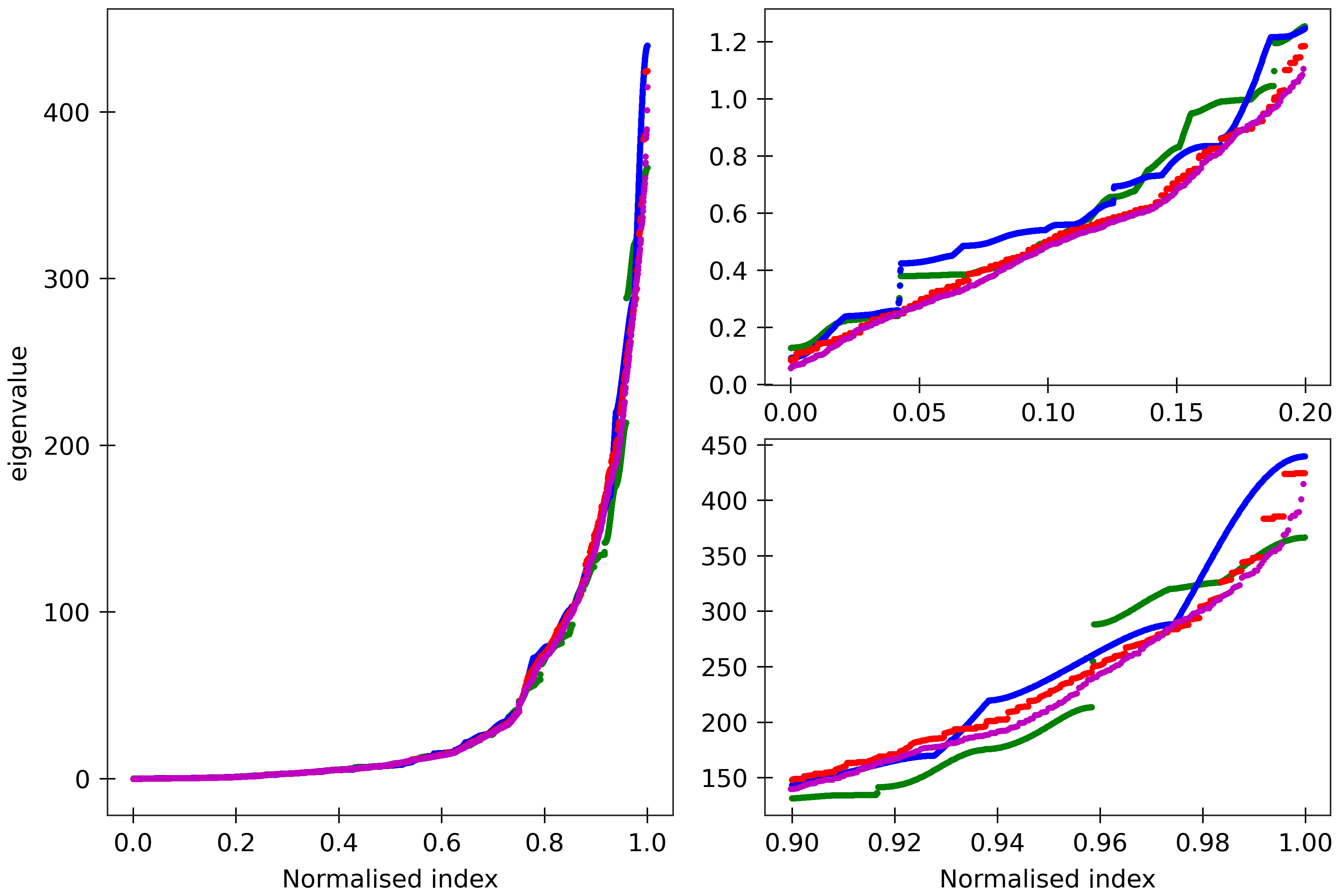
Figure 5 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra (computed using ‘DNA PS2’ parameter set) are here compared for four dsDNA sequences A_300 (blue), (AT)_150 (green), the Widom 601 positioning sequence (magenta) and the A-tract sequence (A_5G_5T_5C_5T)_15 (red). All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

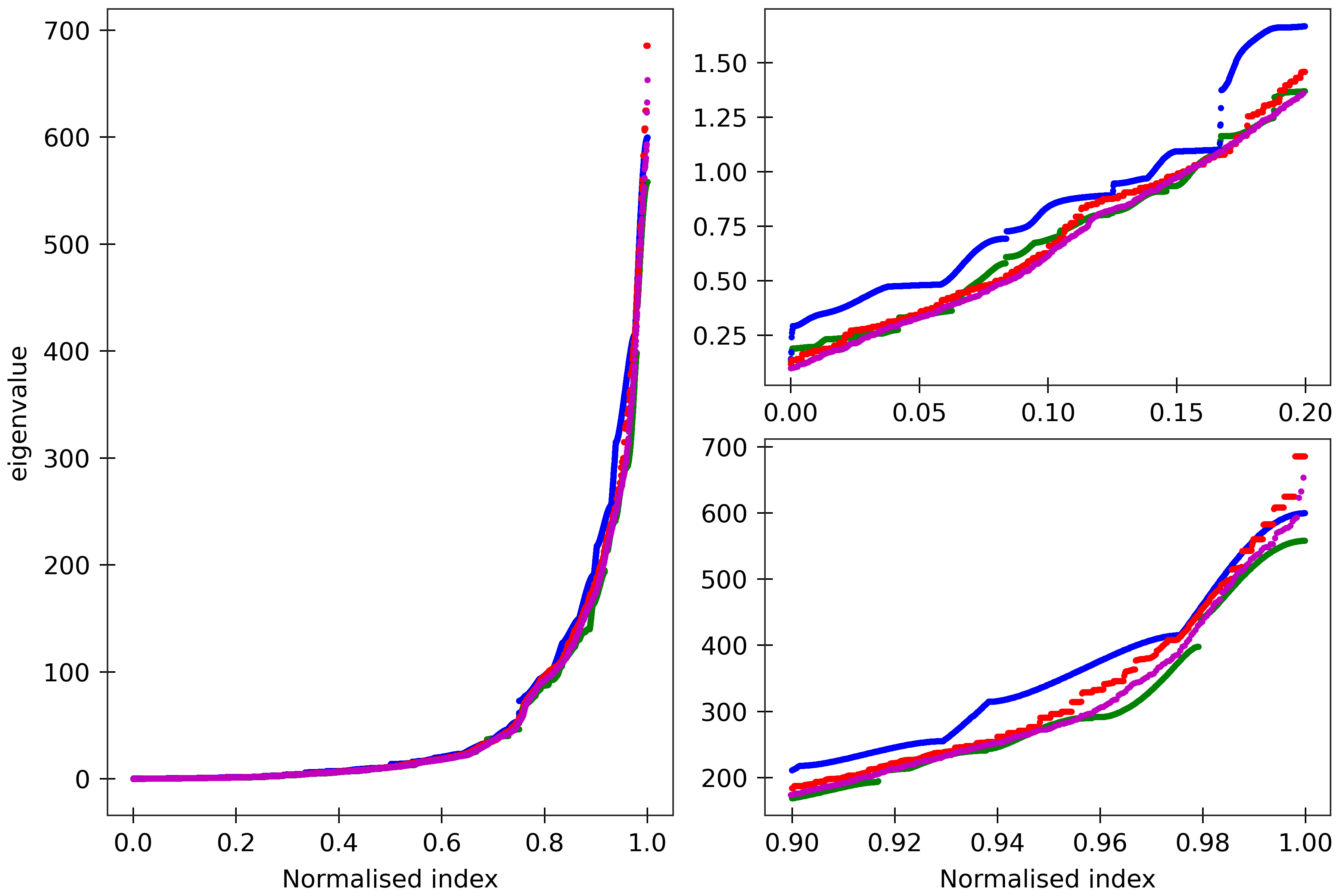
Figure 6 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra (computed using ‘DRH PS2’ parameter set) are here compared for four DRH sequences A_300 (blue), (AT)_150 (green), the Widom 601 positioning sequence (magenta) and the A-tract sequence (A_5G_5T_5C_5T)_15 (red). All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

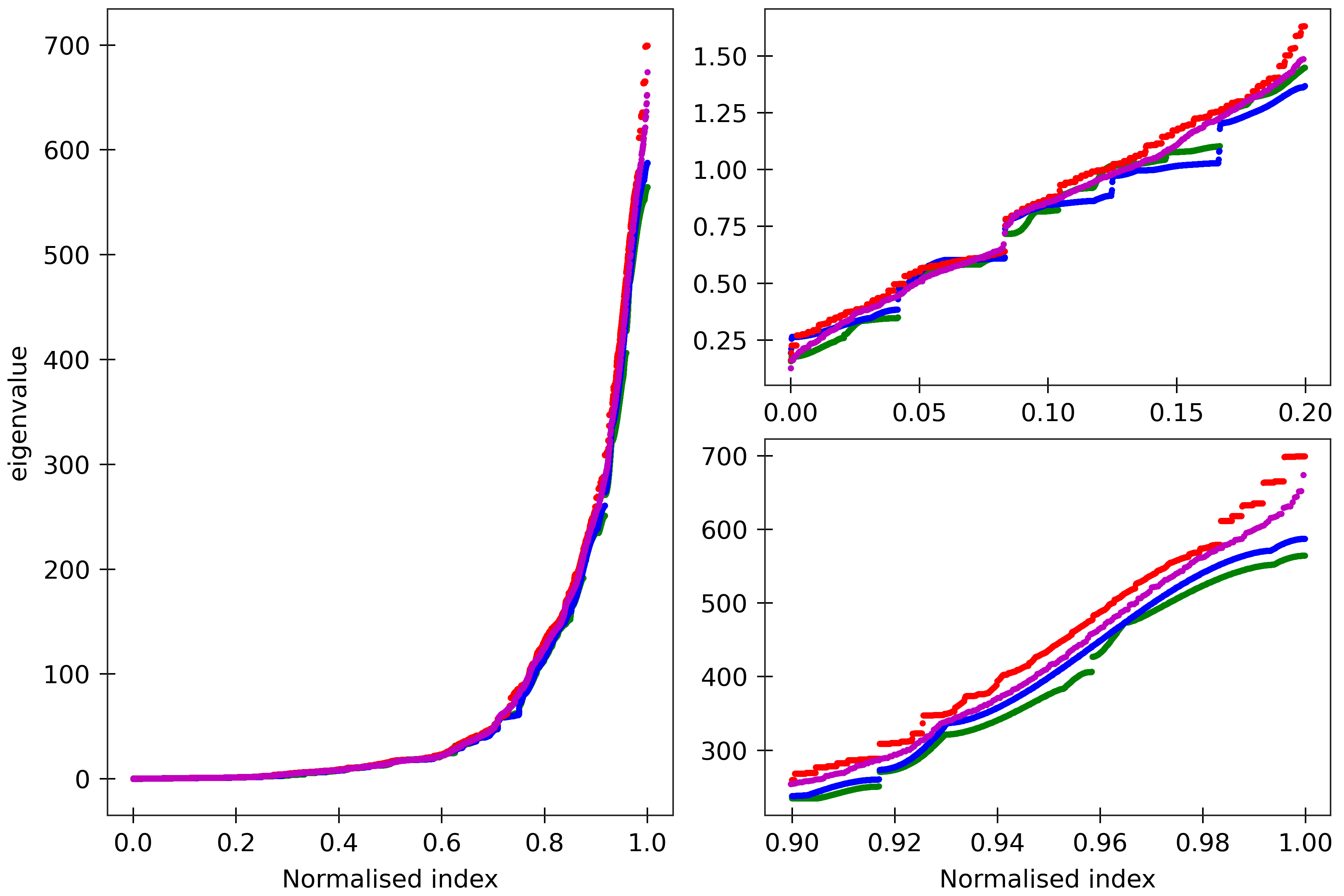
Figure 7 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra (computed using ‘RNA PS2’ parameter set) are here compared for four dsRNA sequences A_300 (blue), (AU)_150 (green), the Widom 601 positioning sequence (magenta) and the A-tract sequence (A_5G_5U_5C_5U)_15 (red). All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

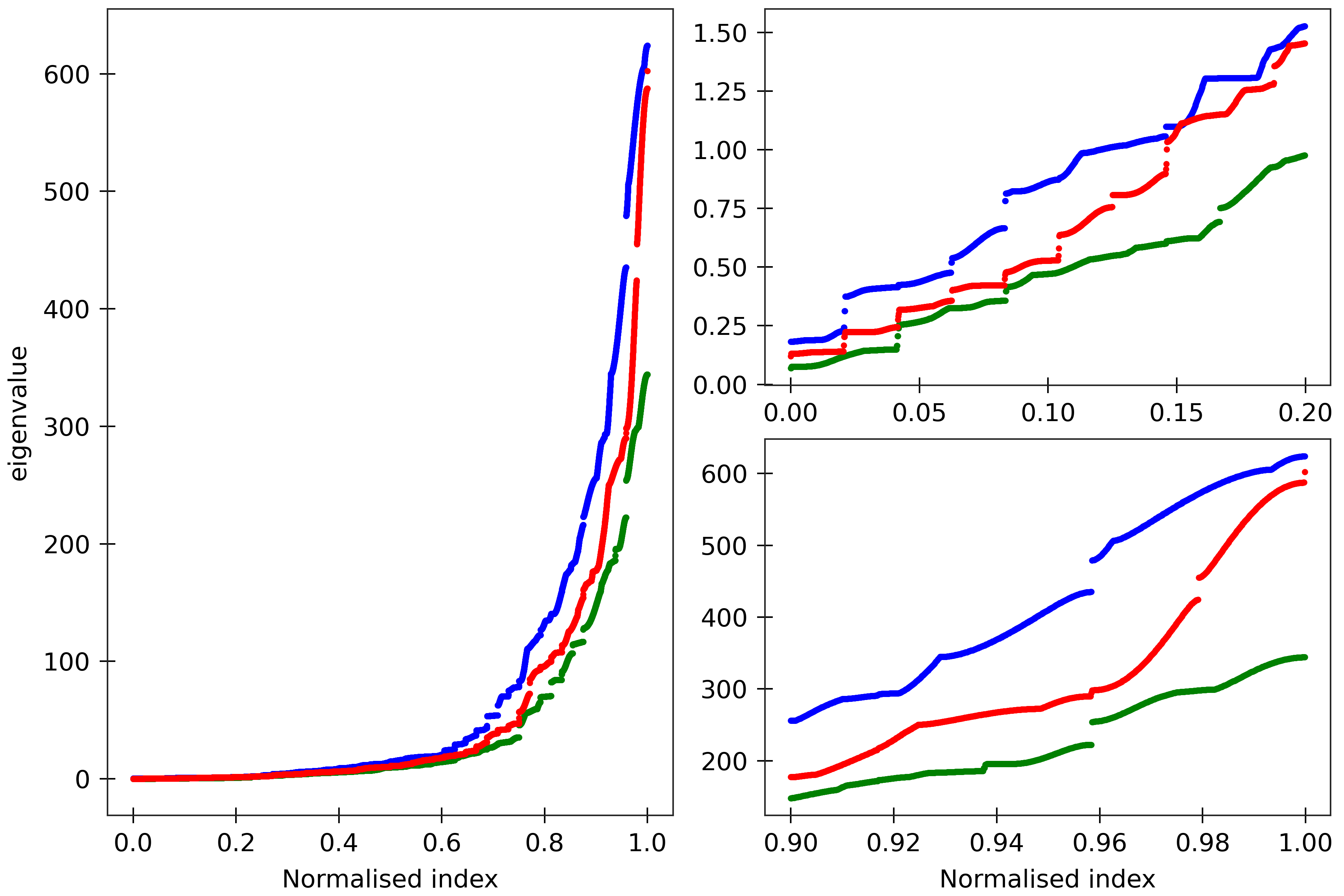
Figure 8 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra are here compared for (CG)_150 for its dsDNA (DNA PS2, green), dsRNA (blue), and DRH (red) versions. All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

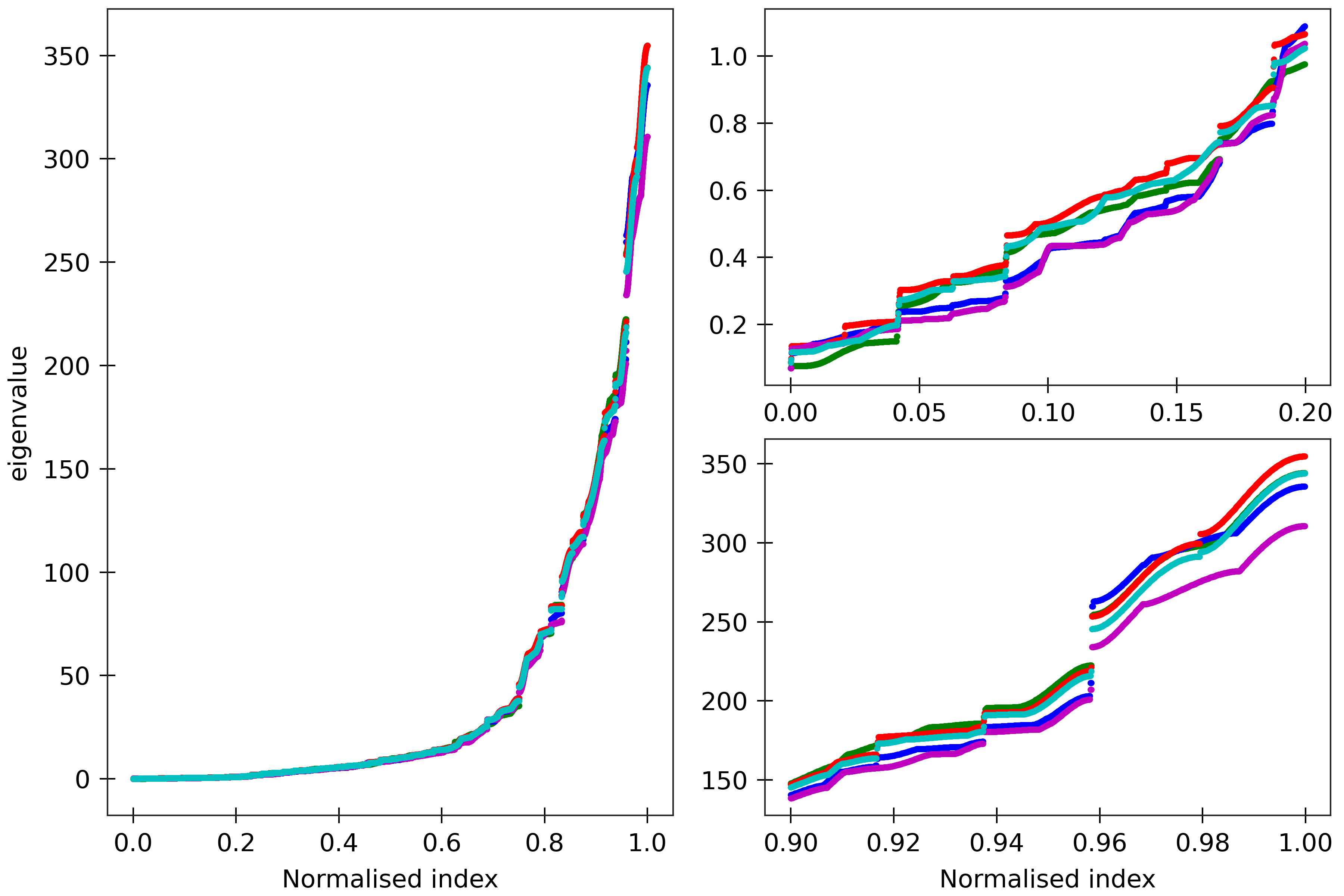
Figure 9 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra are here compared for (CG)_150 (green), (MN)_150 (blue), (MG)_150 (red), (HK)_150 (magenta), and (HG)_150 (cyan). All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

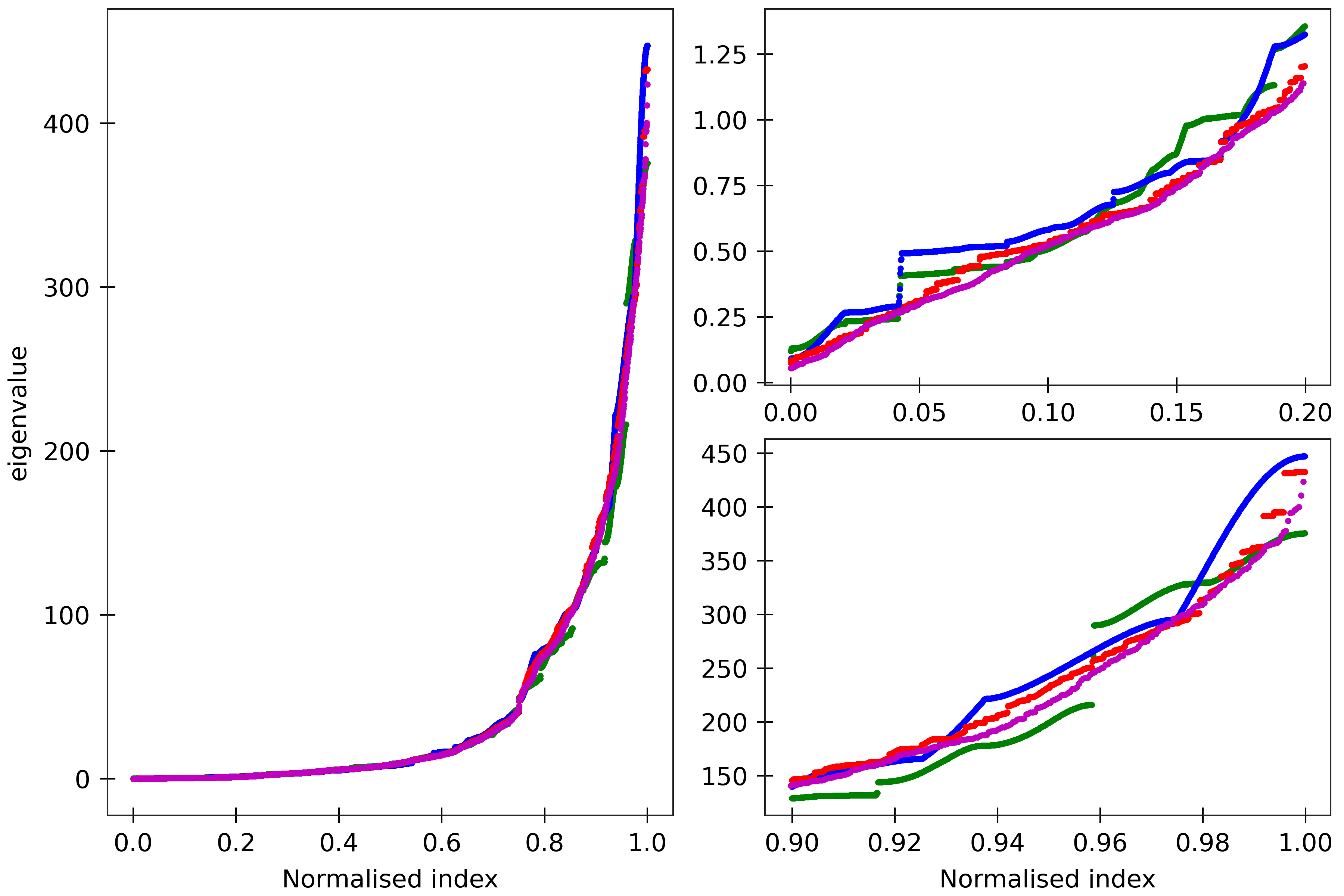
Figure 10 The cgNA+ stiffness matrix for a sequence of length n has 24n-18 eigenvalues, all real and positive, which can be sorted in ascending order and plotted against their index (scaled to always lie in [0,1] to facilitate comparison of spectra for sequences of different lengths). Spectra (computed using ‘DNA PS2’ parameter set) are here compared for four dsDNA sequences A_300 (blue), (AT)_150 (green), the Widom 601 positioning sequence (magenta) and the A-tract sequence (A_5G_5T_5C_5T)_15 (red). All the sequences are taken in GC ends. The two insets on the right are magnifications of the lower and upper parts of the spectra.

Persistence length spectra

Another interesting observable to look at is persistence length which is a popular and traditional quantification of the NA rigidity defined as the length scale over which correlations in the direction of tangent along a polymer centerline are lost. More appropriate definition in the context of sequence-dependence was introduced in Mitchel et. al by factoring out the intrinsic shape contribution from the apparent persistent length (ℓp) to define sequence-dependent dynamic persistence length (ℓd) which solely quantifies the intrinsic rigidity of the NA. Even though it is possible to run MC simulation in the Python and Matlab/Octave version, for heavier computations we recommend C++ code

In this section, we have presented the observed persistence length spectra for millions of dsNA fragments computed using cgNA+mc C++ code. In Figure 7, the top panel plot the spectra for sequence-dependent apparent persistent length (ℓp) and dynamic persistence length (ℓd) while the bottom panel presents histograms for sequence-wise difference in persistence lengths of dsRNA and DRH from dsDNA. The computations were performed for 2 million random sequences of length 220 base-pairs and each computation involved 0.1 million MD samples. Note that the persistence length predicted by the cgNA+ model is, in general, considerably higher than the experimental consensus of 150 bps for dsDNA fragments. But more importantly, as rigorously demonstrated in Mitchel et. al the trends in sequence-dependent persistence lengths of dsDNA are similar to those observed in the experiments. Notably, for shorter sequences (24mer) (refer to A. Patelli's thesis for details), the tangent-tangent correlation observed in the MD simulations is incredibly close to cgNA+ predictions implying that this discrepancy is not inherent to the model. There can be several reasons for this discrepancy of persistence lengths given by cgNA+ tools. Firstly, in experiments, the salt concentration is relatively higher, and often divalent counter ions are used as opposed to mono-valent ions under physiological concentrations in the MD simulations (used to train the cgNA+ model), which have a significant effect on the persistence length of dsDNA (or dsNA). Moreover, the parameterization of DNA in various MD forcefields might be stiffer.

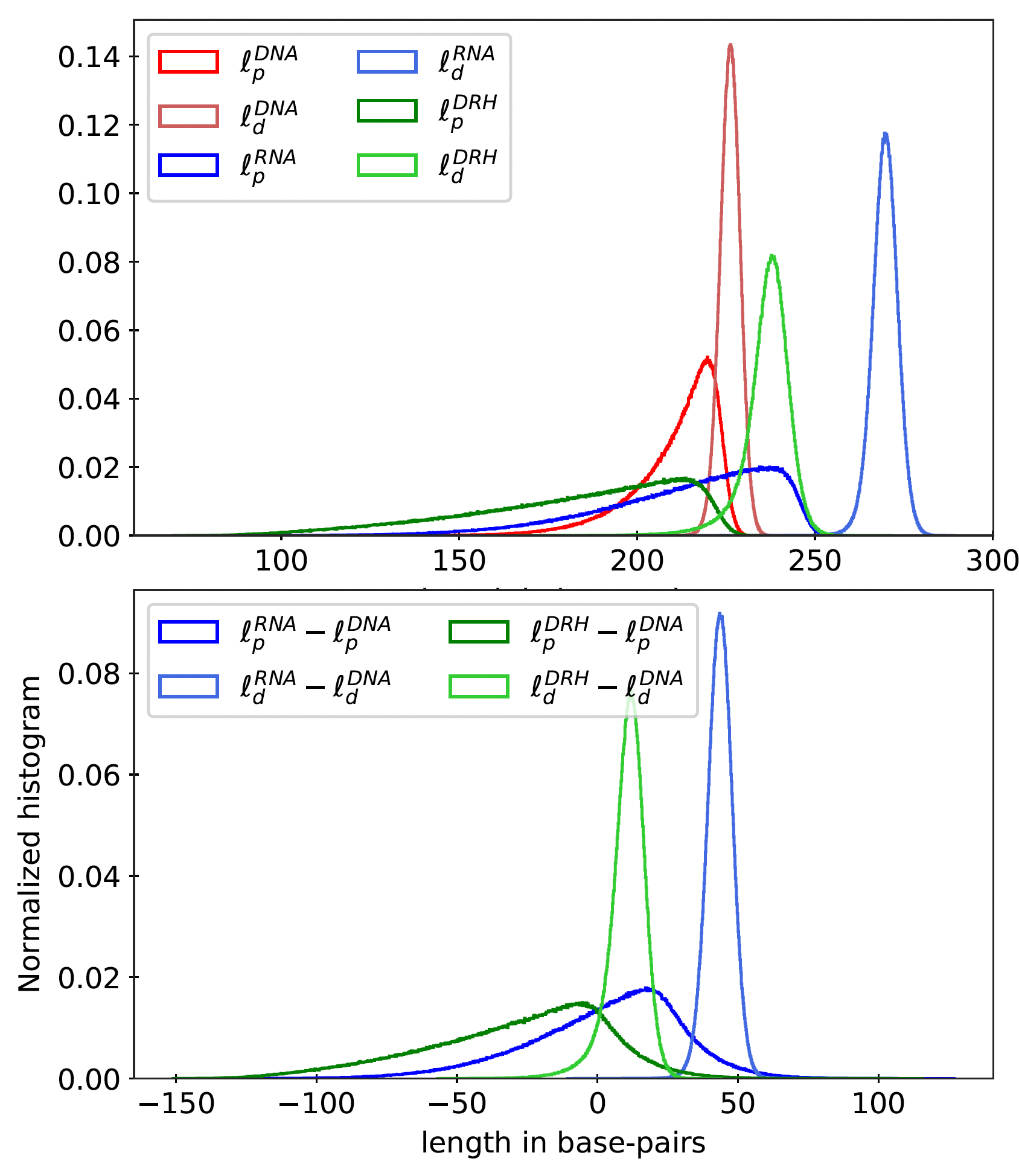
Figure 11 Top: Histogram for dynamic (ℓd) and apparent (ℓp) persistence lengths for ≈ 2 million random sequences (of length 220 bp) and all poly-dimers (110 repeats) for dsDNA, dsRNA, and DRH. Bottom: Histogram for sequence-wise difference in persistence lengths of dsRNA and DRH from dsDNA.

In Figure 8, we have plotted the persistence length of all poly-dimers for various dsNA fragments.

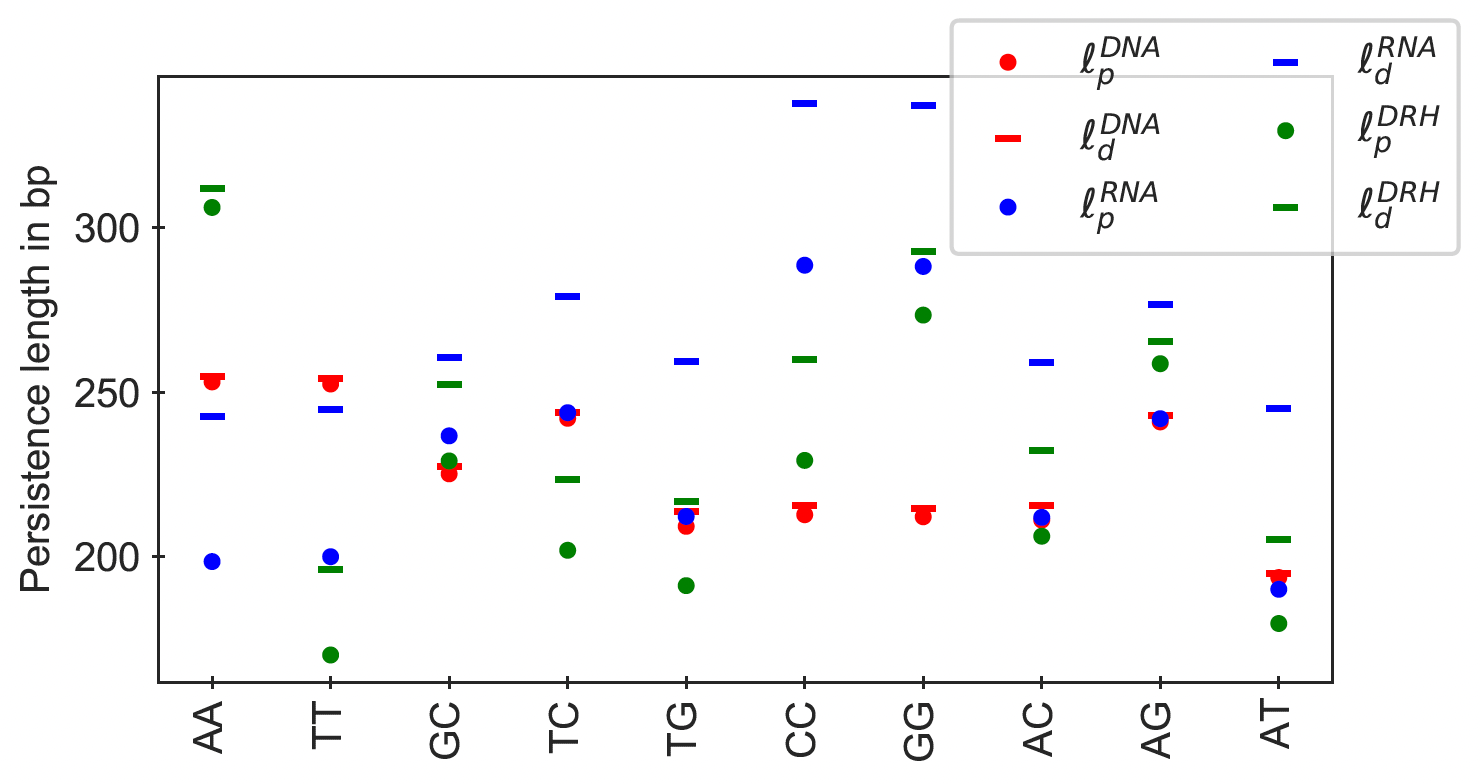
Figure 12 Dynamic (ℓd) and apparent (ℓp) persistence lengths for all independent poly-dimers ((XY)110 embedded in GC ends) for dsDNA, dsRNA, and DRH.

Relevant citations

[1] cgNA+web: A web based visual interface to the cgNA+ sequence dependent statistical mechanics model of double-stranded nucleic acids.
R. Sharma, A. S. Patelli, L. De Bruin, and J.H. Maddocks
Journal of Molecular Biology, 167978 (2023)
DOI:10.1016/j.jmb.2023.167978

[2] cgNA+: A sequence-dependent coarse-grain model of double-stranded nucleic acids.
R. Sharma, EPFL Thesis #9792 (2022)
Download the PDF here.

[3] A sequence-dependent coarse-grain model of B-DNA with explicit description of bases and phosphate groups parametrised from large scale Molecular Dynamics simulations
A.S. Patelli
EPFL PhD Thesis #9552 (2019)
PDF available here

[4] cgDNAweb: a web interface to the cgDNA sequence-dependent coarse-grain model of double-stranded DNA.
L. De Bruin, J.H. Maddocks
Nucleic Acids Research 46, issue W1 (2018), p. W5-W10
DOI:10.1093/nar/gky351

[5] Absolute versus relative entropy parameter estimation in a coarse-grain model of DNA
O. Gonzalez, M. Pasi, D. Petkevičiūtė, J. Glowacki, J.H. Maddocks
Multiscale Modeling and Simulation 15, no. 3 (2017), p. 1073 - 1107
DOI:10.1137/16M1086091

[6] Sequence-Dependent Persistence Lengths of DNA
J.S. Mitchell, J. Glowacki, A.E. Grandchamp, R.S. Manning, J.H. Maddocks
Journal of Chemical Theory and Computation 13 (2017), p. 1539-1555
DOI:10.1021/acs.jctc.6b00904

[7] cgDNA: a software package for the prediction of sequence-dependent coarse-grain free energies of B-form DNA
D. Petkevičiūtė, M. Pasi, O. Gonzalez, J.H. Maddocks
Nucleic Acids Research 42, no. 20 (2014), p. e153
DOI:10.1093/nar/gku825

[8] μABC: a systematic microsecond molecular dynamics study of tetranucleotide sequence effects in B-DNA
M. Pasi, J.H. Maddocks, D. Beveridge, T.C. Bishop, D.A. Case, T. Cheatham III, P.D. Dans, B. Jayaram, F. Lankas, C. Laughton, J. Mitchell, R. Osman, M. Orozco, A. Pérez, D. Petkevičiūtė, N. Spackova, J. Sponer, K. Zakrzewska, R. Lavery
Nucleic Acids Research 42, no. 19 (2014), p. 12272–12283
DOI:10.1093/nar/gku855

[9] A sequence-dependent rigid-base model of DNA
O. Gonzalez, D. Petkevičiūtė, J.H. Maddocks
Journal of Chemical Physics 138, no. 5 (2013), p. 055122 1-28
DOI:10.1063/1.4789411

How to cite

If you use this website in relation to any publication please cite:

cgNA+web: A web based visual interface to the cgNA+ sequence dependent statistical mechanics model of double-stranded nucleic acids
R. Sharma, A. S. Patelli, L. De Bruin, and J.H. Maddocks
Journal of Molecular Biology, 167978 (2023)
DOI:10.1016/j.jmb.2023.167978

The cgNA+web site is an evolution from a pre-cursor site (still available at https://cgdnaweb.epfl.ch/view2) and is described in:

cgDNAweb: a web interface to the cgDNA sequence-dependent coarse-grain model of double-stranded DNA.
L. De Bruin, J.H. Maddocks
Nucleic Acids Research 46, issue W1 (2018), p. W5-W10
DOI:10.1093/nar/gky351

The current updated cgNA+web version is an interface to the enhanced coarse-grain model cgNA+ of sequence-dependent statistical mechanics of double-stranded nucleic acids. cgNA+ includes parameter sets for dsDNA in an epigenetic sequence alphabet, dsRNA, and DNA:RNA hybrid as described in detail in

cgNA+: A sequence-dependent coarse-grain model of double-stranded nucleic acids.
R. Sharma, EPFL Thesis #9792, Under the supervision of J. H. Maddocks
Download the PDF here.

The extended cgNA+ parameter sets are built on the cgDNA+ model, which itself extends the original cgDNA model by the inclusion of an explicit description of phosphate groups. The cite for the cgDNA+ model itself is:

A sequence-dependent coarse-grain model of B-DNA with explicit description of bases and phosphate groups parametrised from large scale Molecular Dynamics simulations.
A. S. Patelli, EPFL Thesis #9522, Under the supervision of J. H. Maddocks
Download the PDF here.

More generally the cgDNA family of models has its own web page, which includes citations to all other related codes and articles.

Contact

Prof. John H. Maddocks
MATH-FSB-EPFL, Station 8
Swiss Federal Institute of Technology
CH-1015 Lausanne
@: john (dot) maddocks (at) epfl (dot) ch

Credits

Original code by L. de Bruin (debruin (at) lorentz (dot) leidenuniv (dot) nl), and P. Voirol (philippe.voirol (at) epfl (dot) ch), with the help of A. S. Patelli (alessandro.patelli (at) epfl (dot) ch) and R. Sharma (rahul.sharma (at) epfl (dot) ch) for later enhancements. Original concept by J. H. Maddocks, site designed and developed jointly. Thanks also to other members of the LCVMM, particularly T. Zwahlen, R. Singh, and Masters students at the EPFL for testing and debugging the site.

Development of the web site was financially supported by the EPFL and the Swiss National Science Foundation under Award 200020 143613/1 and 200020-18218 to JHM.

Getting started

cgNA+web is an interface to allow interactive visualisation of the sequence-dependent ground state, or free energy minimizing, configuration of a nucleic acid double helical fragment as predicted by the cgNA+ model. cgNA+web is an evolution from the prior, analogous, interface cgDNAweb.

The cgNA+web interface is primarily aimed at visualising the sequence-dependent minimum free energy, or ground state, configuration in the Gaussian equilibrium distribution that is predicted by the cgNA+ model (see cgNA+ model panel for more details). The ground state can be visualised either in the 2D Plots pane, as graphs of the internal coordinates along the sequence, or in the 3D View pane as the 3D configuration visualised at various levels of detail.

How to use cgNA+web

Fill in a dsNA sequence in the input form of the header at the top of the web page (try starting by typing a 10-20 bp long fragment, or you can copy paste much longer sequences; up to 3Kbp or so are feasible on a contemporary laptop). Hard limits for the website to function, are that the input sequences need to be at least four basepairs long and less than 3Kbp. The input format is either a string of nucleotides from the {A,C,G,T/U} alphabet or modified CpG steps {MN, MG, CN, HK, HG, CK} alphabets, (upper or lower case, which can be mixed, and with or without spaces). However, the input must respect the following rules for various dsNA parameter sets:

- DNA PS2: input sequence must be a string from {A,T,C,G} alphabet or modified
  CpG steps {MN, MG, CN, HK, HG, CK} alphabets but modified CpG steps
  can not be terminal base-pair step and hydroxymethylated and methylated steps
  can not be adjacent to each other, e.g. MNHK, HKMN, etc not allowed but
  MNMN, HKHG, etc allowed.
- RNA PS2: input sequence must be a string from {A,T/U,C,G} alphabet but then T
  will be internally modified to U
- DRH PS2: input sequence must be a string from {A,T,C,G} alphabet with GC
  ends, if not, then cgNA+web will add GC end(s) to the input sequence
- DNA PS1: input sequence must be a string from {A,T,C,G} alphabet
- cgDNA: input sequence must be a string from {A,T,C,G} alphabet

where A, T, C, G, U are standard alphabets nucleic bases representing Adenine, Thymine, Cytosine, Guanine, and Uracil, while M and H represent methylated C and hydroxymethylated C, respectively and H and K represent G when the complementary C is methylated and hydroxymethylated, respectively. So, for example, one can type 'A atCG c' for a linear fragment or, for tandem repeats, a sequence between parentheses, and a number after an underscore, e.g. A_12 for the homopolymer poly(A) of length 12 or (AG)_100 for the alternating poly(AG) molecule with 200 basepairs. For each dsNA, we recommend using the PS2 parameter set, which we regard as the current state of the art. The default setting is DNA PS2 (for dsDNA including epigenetic base modifications) and one has to then choose the parameter set for other kind of dsNAs from the dropdown menu.

The input characters are all considered to be ASCII, and in principle carriage returns, newlines, spaces, and tabs may be included in the input and are all ignored. Attention to copy pasting from PDF documents where other hidden characters may be included, and cause rejection of the input. The border of the input form turns red when the input is rejected, either because of length constraints, unrecognised characters or unmatched parentheses.

Then click "Go", and inspect the Output in either the 3D View or 2D Plots panes.

cgNA+web can visualise superpositions of ground states for up to four different cases simultaneously, e.g. ground states of different sequences of the same dsNA, or analogous sequences of different dsNAs, or differences for the same sequence with different parameter sets (this feature is currently only available for dsDNA) can be compared. To make multiple sequence inputs, use the arrow keys to switch to another input form, or click one of the white dots. A maximum of four sequences can be visualised at one time, but each of the four sequences can be modified and re-plotted individually (the sequence input in the form box is deleted by clicking the x button, along with its associated plots and visualisations). Specific base pair frames of different sequences will be aligned in the 3D viewer whenever a particular nucleotide is wrapped in square brackets in the input sequence, e.g. A_6 [T] A_6. In this case, the viewer will have the basepair with base T on the reading strand at the centre of the view. Note that there can be at most one set of brackets [ ] per sequence; therefore it is not possible to use this syntax within tandem repeats. No explicit [ ] in the input sequence defaults to the first base pair frame being taken for centring.

Some documentation

Given the input sequence, and a selected parameter set from the dropdown menu next to the sequence input, you can view the ground state of the dsNA in the '3D View' tab or in the '2D Plots' tab. Once a sequence or sequences have been entered, the arrow on the right of the darker blue navigation bar can be used to show or hide the the header panel for more or less viewing space.

Viewer controls

The controls for the 3D viewer are mainly mouse-based:

Rotate

left click and drag, or single finger drag on mobile.

Zoom

middle mouse click, scroll, or pinch on mobile.

Pan

shift+left click and drag, or triple finger drag on mobile.

Context menu

Accessed by right click or command+click on macOS, the viewer context menu gives access to:

Center on this base

Rotates and translates the dsNA such that the base frame of the selected base coincides with the origin.

Center on this base pair

Rotates and translates the dsNA such that the base pair frame of the selected base coincides with the origin.

Look at center/origin

Rotates the camera such that the origin is centred in the viewport.

Reset Zoom/Orientation

Reset any Zoom or Orientation applied by the user.

Selecting the gear icon in the 3D view pane provides various viewing options. The cgNA+ model assumes rigid bases and rigid phosphate groups. Each base can be visualised as its individual (heavy) atoms, or as a (red) frame (i.e. an origin and three orthonormal vectors embedded in the base according to Curves+ conventions), or as a box surrounding the base atoms, colour coded for sequence, and differently sized for purines and pyrimidines. The Curves+ base pair, which is an appropriate average of the two associated rigid bases, can also be visualised as either a (grey) frame or a surrounding bicolour box. Similarly each phosphate group can be visualised as a tetrahedron, or with its component atoms drawn in idealised relative positions. The cgNA+ model treats sugar rings only implicitly, so they cannot be visualised explicitly in cgNA+web. (When a cgDNA, not cgNA+, paramset is selected in cgNA+web there is no explicit treatment of phosphates, and the backbones are visualised via a simple numerical interpolation of the base frame positions.) When any base or phosphate is selected with the mouse, an inset window reports the strand location and composition of the base in the associated nucleotide. The 3D view is centred on the basepair frame selected by [ ] in the input sequence, and this frame is highlighted by a larger RGB frame.

Sufficiently long sequences eventually can become unwieldy to manipulate interactively in the 3D viewer, particularly when visualising individual atoms, and depending on the particular hardware being used. However long length-scale ground states for sequences of the order of 3Kbp in length can still be reconstructed with cgNA+web and nontrivial, overall shapes observed in some sequences. For example the phased A-tract tandem repeat sequence of 840=40x21 bp (a_5 g_5 t_5 c_5 g)_30 a_5 g_5 t_5 c_5 [g](a_5 g_5 t_5 c_5 g)_19 (here the particular syntax centres the 3D view toward the centre of the sequence) can still be reconstructed via the web server and locally viewed (e.g. on a 2015 Macbook Pro) to reveal a strong superhelical ground state.

2D plots pane

In this pane, the first set of 12 panels provide ground state values of the standard twelve Curves+ helicoidal internal coordinates for the bases (6 inter base-pair, or junction, coordinates, and 6 intra base-pair coordinates, each with three translation and three rotational degrees of freedom) plotted along each input sequence. Translational coordinates are reported in Å with rotational coordinates (or components of the rotational Cayley vector) reported either in degrees or in cgNA+ internal units of 1/5 radians or approximately 11 degrees. (This nonstandard rotational unit gives a good scaling between rotational and translational stiffnesses of dsNA in the underlying Gaussian coarse-grain model.)

In cgNA+web the second set of 12 panels provide ground state values of the 2x6 = 12 coordinates (six translation and six rotation degrees of freedom) of the relative rigid body displacement of each phosphate group from the base in its nucleotide. The 5' phosphate coordinates are for the phosphate group in the backbone of the reading (or Watson) strand, which for basepair n lies in the junctions between the (n-1)th and nth base pair. The 3' phosphate coordinates are for the phosphate group in the backbone of the complementary (or Crick) strand, which for basepair n lies in the junction between the nth and (n+1)st base pair.

Placing the cursor over any one of the 2D plots returns the numerical values in the plot along with the local sequence context. For very long sequences the 2D plots typically become less visually less useful, but the numerical data can still be accessed via the mouse cursor.

Parameter sets

Parameters in the cgNA+ model are estimated from large scale libraries of Molecular Dynamics (or MD) simulations. Specific cgNA+ parameter sets have been estimated for dsDNA in both standard and epigenetically modified alphabets, for dsRNA, and for DRH. Each parameter set corresponds to a specific MD simulation protocol, capturing, for example, the species and concentration of counter ions in the solvent, and of course the specific MD force field (specific to the kind of dsNA), water model, etc. Different MD simulation force fields and protocols may lead to different atomistic equilibrium distributions, which also get reflected in cgNA+ parameter sets. Currently, we have two different cgNA+ parameter sets for dsDNA (DNA PS1 and DNA PS2) corresponding to two different MD protocols (listed below). Finally, the cgNA+ model itself continues to be actively developed in various directions, in particular, more parameter sets will continue to be developed, for example, a parameter set that allows base-pair mismatches in dsDNA or dsDNA parameter sets trained on MD simulations with updated MD protocol (by ABC) are currently being developed. cgNA+web will, in due course, be updated accordingly and the parameter set will be described here. The current cgNA+ parameter set are the following:

• [cgDNA] cgDNA (old model)
  • Palindromic sequence library
  • 3 microseconds of Amber MD time series
  • bsc1 force field
  • 150mM of K+ counter-ions
  • Maximum entropy/likelihood truncation
  • Fitting functional: Kullback-Leibler divergence with model pdf in first argument
  • Dinucleotide model with specific blocks for the dimers at the ends
• [DNA (PS1)] DNA PS1 (cgDNA+ model)
  • Palindromic sequence library
  • 3 microseconds of Amber MD time series
  • bsc1 force field and SPC/E water model
  • 150mM of K+ counter-ions (Dang parameters)
  • Maximum entropy/likelihood truncation
  • Fitting functional: Kullback-Leibler divergence with model pdf in first argument
  • Dinucleotide model with specific blocks for the dimers at the ends
• [DNA (PS2)] DNA PS2 (cgNA+ model, recommended)
  • Palindromic sequence library
  • 10 microseconds of Amber MD time series
  • bsc1 force field, TIP3P water model
  • 150mM of K+ counter-ions (Joung and Cheatham parameters)
  • Maximum entropy/likelihood truncation
  • Fitting functional: Kullback-Leibler divergence with model pdf in first argument
  • Dinucleotide model with specific blocks for the dimers at the ends
  • Also, contains parameters for modified CpG steps
  • C is referred to as M and H when methylated and hydroxymethylated, respectively and
  • G is referred to as N and K when complementary C is methylated and hydroxymethylated, respectively
  • Note only CpG steps can be modified i.e. allowed steps are MN, MG, CN or HK, HG, CK
  • hydroxymethylated and methylated steps are allowed in the same sequence but not adjacent
• [RNA (PS2)] RNA PS2 (cgNA+ model, recommended)
  • Palindromic sequence library
  • 10 microseconds of Amber MD time series
  • OL3 force field, TIP3P water model
  • 150mM of K+ counter-ions (Joung and Cheatham parameters)
  • Maximum entropy/likelihood truncation
  • Fitting functional: Kullback-Leibler divergence with model pdf in first argument
  • Dinucleotide model with specific blocks for the dimers at the ends
  • input accepts both U and T but then internally change T to U
• [DRH (PS2)] DNA:RNA Hybrid (DRH) PS2 (cgNA+ model, recommended)
  • Same sequence library but not palindromic
  • 10 microseconds of Amber MD time series
  • bsc1 and OL3 force field for DNA and RNA strand, respectively, TIP3P water model
  • 150mM of K+ counter-ions (Joung and Cheatham parameters)
  • Maximum entropy/likelihood truncation
  • Fitting functional: Kullback-Leibler divergence with model pdf in first argument
  • Dinucleotide model with specific blocks for the dimers at the ends
  • Only accepts sequence in A, T, C, G and must be with GC ends

Export pane

It is possible to export the configuration and other data in multiple ways, by selecting an entry in the 'Export' menu.

Atom coordinates as .pdb

This will download a .pdb format file with all of the heavy atoms in the DNA bases and phosphate groups. The base atoms have positions as specified by the Tsukuba convention within the base, with an analogous convention for the phosphate group atoms. Note that, due to the available character length in the PDB format specification for atom coordinates, the output generated directly here for long DNA molecules may be incorrect. Up to 300bp or so in length is a conservative estimate below which no problem will arise. Absolute coordinates of phosphate, base and basepair frame origins are still available for longer length molecules in the .fra output format. And from .fra output absolute PDB coordinates of each atom can be computed locally by suitably modifying available cgNA+ scripts.

Frames as .fra/.pfra file

This will download a Curves+ .fra and .pfra format file describing the configuration of coordinate frames in the molecule. For both formats, the file contains one line per frame and each line contains the following columns: <no of strand> <no of basepair> <d1_1> <d1_2> <d1_3> <d2_1> <d2_2> <d2_3> <d3_1> <d3_2> <d3_3> <r_1> <r_2> <r_3> where the triples d1,d2,d3 are the (absolute, or laboratory, nondimensional) coordinates of the three vectors making up each orthonormal frame, and r is the (absolute) position of the frame (in Angstroms). The .fra file contains all the base frames while .pfra contains all the phosphate group frames.

Basepair frames as .fra file

The same as above, but for the base-pair frames.

Shapes as .svg

Downloads a zipped graphics file with all the plots of the internal coordinates as they are shown in the '2D Plots' tab, but without the interactivity.

Shapes as .txt

Downloads the internal configuration of the molecule as it appears in the cgDNA model. That is, a column vector containing (x_1,C_1,y_1,W_2,x_2,C_2,..., y_{n-1},W_{n-1}, x_n), where x_i, y_i, W_i, and C_i are real 6-vectors, and x_i contains the 6 intra coordinates, y_i the 6 inter coordinates, W_i the 6 reading strand base-to-phosphate coordinates, C_i the complementary strand base-to-phosphate coordinates, with translations in Angstrom, and the rotations in rad/5.

Stiffness matrix in CSC format, stored in JSON

This will download a zipped file with all the stiffness matrices of the input sequences in compressed sparse column format in a JSON file. This can be used by SciPy by also using the built in JSON decoder.

Browser support

Resources used

This website used three.js for visualisation of dsNA. Plots are generated with the help of d3.js. Symbols shown are from Font Awesome. Zips are generated with JSZip. Files are saved with FileSaver.js. Linear algebra calculations done with Armadillo. jQuery is also involved.

The cgNA+web code (both front- and back-end) is available here.